News from this site

Rental advertising space, please contact the webmaster if you need cooperation

article

24152

browse

+focus

classification

no classification

date

2024-11(11)

[Operational Research and Optimization] Detailed Explanation of Vehicle Path Planning Problem with Time Window Constraints (VRPTW) + Python Call Gurobi Modeling Solution

posted on 2023-06-06 10:24 read(605) comment(0) like(19) collect(4)

Article Directory

I. Overview
2. The general model of VRPTW
3. Python calls Gurobi to model and solve

I. Overview

1.1 VRP problem

Vehicle routing problem (Vehicle Routing Problem, VRP) generally refers to: for a series of delivery points and receiving points, organize and call certain vehicles, arrange appropriate driving routes, so that vehicles pass through them in an orderly manner, and meet the specified Under certain constraints (for example: demand and delivery of goods, delivery time, vehicle capacity limitation, driving mileage limitation, driving time limitation, etc.), strive to achieve certain goals (such as the shortest total mileage of empty vehicles, the total transportation time, etc.) The cost is the lowest, vehicles arrive at a certain time, the number of vehicles used is the smallest, etc.).

The figure below gives an example of a simple VRP

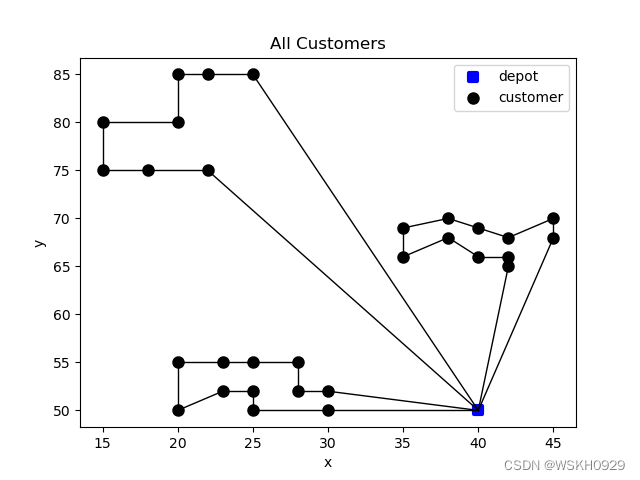
insert image description here

1.2 CVRP problem

The most basic VRP problem is called the Capacitated Vehicle Routing Problem (CVRP). In CVRP, the capacity constraints of each vehicle, the path constraints of the vehicles and the load constraints need to be considered

1.3 VRPTW problem

In order to consider the delivery time requirements, the vehicle routing problem with time window (Vehicle Routing Problem with Time Window, VRPTW) came into being.

VRPTW not only considers all constraints of CVRP, but also needs to consider time window constraints, that is, each customer corresponds to a time window $e_i,l_i]$ ,in $e_i$ and $l_i$ Represent the earliest arrival time and latest arrival time of the point, respectively. customer point $\in V$ The demand must be served within its time window

VRPTW has been proven to be an NP-hard problem, and its solution complexity increases sharply with the increase of the problem size, making it difficult to solve. So far, the more efficient and accurate algorithms for solving VRPTW are the branch pricing algorithm and the branch pricing and cutting algorithm.

2. The general model of VRPTW

VRPTW can be modeled as a mixed integer programming problem. Before giving the complete mathematical model, the following decision variables are introduced:

${x_i}_j=$

{\begin{cases} 1, if in the optimal solution, the arc (i, j) by vehicle k selected \\ 0,other \end{cases}

$\begin{cases} 1\text{，如果在最优解中，弧}\left( i,j \right) \text{被车辆}k\text{选中}\\ 0\text{，其他}\\ \end{cases}$ \\ {s_i}_k=\text{vehicle}k\text{time of arrival}i\text{} \\ \text{The other parameters involved in the model are}: \\ {t_i}_j\text{represents the vehicle The travel time on the arc}\left( i,j \right) \text{} \\ M\text{is a sufficiently large positive number}

x_{i}_{j} = {1, if in the optimal solution, the arc (i, j) selected by vehicle k 0, other s_{i}_{k} = The time when vehicle k arrives at i Other parameters involved in the model are : t_{i}_{j} Indicates that the vehicle is on the arc (i, j) drive time on M is a sufficiently large positive number

Regarding the value of M, in fact, a very large positive number can be taken directly, but in order to improve the solution efficiency, the constraints are tightened. We can use the following value method:

$M=max\{b_i+t_{ij}-a_j\} , \forall (i,j)\in A$

Combining the above-mentioned decision variables and referring to literature (Desaulniers et al., 2006), the standard model of VRPTW is given as follows:

$\min \sum_{k\in K}{\sum_{i\in V}{\sum_{i\in V}{{c_i}_j{x_i}_{j_k}}}} \\ s.t. \sum_{k\in K}{\sum_{j\in V}{{x_i}_{j_k}=1 , \forall i\in C}} \\ \,\, \sum_{j\in V}{{x_0}_{j_k}=1 , \forall k\in K} \\ \,\, \sum_{i\in V}{{x_i}_{h_k}-\sum_{j\in V}{{x_h}_{j_k}=0 , \forall h\in C,\forall k\in K}} \\ \,\, \sum_{i\in V}{x_{i,n+1,k}=1 , \forall k\in K} \\ \,\, \sum_{i\in C}{q_i\sum_{j\in V}{{x_i}_{j_k}=1 , \forall k\in K}} \\ \,\, {s_i}_k+{t_i}_j-M\left( 1-{x_i}_{j_k} \right) \leqslant {s_j}_k\,\,, \forall \left( i,j \right) \in A,\forall k\in K \\ \,\, e_i\leqslant {s_i}_k\leqslant l_i\,\,, \forall i\in V,\forall k\in K \\ \,\, {x_i}_{j_k}\in \left\{ 0,1 \right\} \,\,, \forall \left( i,j \right) \in A,\forall k\in K$

in:

The objective function is to minimize the total travel cost (distance) of all vehicles
Constraints 1~4 ensure that each car must start from the warehouse, leave that point after passing through a point, and finally return to the warehouse
Constraint 5 is the capacity constraint of the vehicle
Constraints 6~7 are time window constraints, which ensure that the time when the vehicle arrives at each customer point is within the time window. Point n+1 is a backup of point o, for the convenience of realization.

3. Python calls Gurobi to model and solve

3.1 Solomn Dataset

Solomn dataset download address

3.2 Complete code

Note that in the code below, the arc $i$ to the arc $j$ time required $t_{ij}$ and cost $c_{ij}$ all as an arc $i$ to the arc $j$ required distance to see

# -*- coding: utf-8 -*-#
# Author: WSKH
# Blog: wskh0929.blog.csdn.net
# Time: 2023/2/8 11:14
# Description: Python 调用 Gurobi 建模求解 VRPTW 问题
import time
import matplotlib.pyplot as plt
import numpy as np
from gurobipy import *


class Data:
    customerNum = 0
    nodeNum = 0
    vehicleNum = 0
    capacity = 0
    corX = []
    corY = []
    demand = []
    serviceTime = []
    readyTime = []
    dueTime = []
    distanceMatrix = [[]]


def readData(path, customerNum):
    data = Data()
    data.customerNum = customerNum
    if customerNum is not None:
        data.nodeNum = customerNum + 2
    with open(path, 'r') as f:
        lines = f.readlines()
        count = 0
        for line in lines:
            count += 1
            if count == 5:
                line = line[:-1]
                s = re.split(r" +", line)
                data.vehicleNum = int(s[1])
                data.capacity = float(s[2])
            elif count >= 10 and (customerNum is None or count <= 10 + customerNum):
                line = line[:-1]
                s = re.split(r" +", line)
                data.corX.append(float(s[2]))
                data.corY.append(float(s[3]))
                data.demand.append(float(s[4]))
                data.readyTime.append(float(s[5]))
                data.dueTime.append(float(s[6]))
                data.serviceTime.append(float(s[7]))
    data.nodeNum = len(data.corX) + 1
    data.customerNum = data.nodeNum - 2
    # 回路
    data.corX.append(data.corX[0])
    data.corY.append(data.corY[0])
    data.demand.append(data.demand[0])
    data.readyTime.append(data.readyTime[0])
    data.dueTime.append(data.dueTime[0])
    data.serviceTime.append(data.serviceTime[0])
    # 计算距离矩阵
    data.distanceMatrix = np.zeros((data.nodeNum, data.nodeNum))
    for i in range(data.nodeNum):
        for j in range(i + 1, data.nodeNum):
            distance = math.sqrt((data.corX[i] - data.corX[j]) ** 2 + (data.corY[i] - data.corY[j]) ** 2)
            data.distanceMatrix[i][j] = data.distanceMatrix[j][i] = distance
    return data


class Solution:
    ObjVal = 0
    X = [[]]
    S = [[]]
    routes = [[]]
    routeNum = 0

    def __init__(self, data, model):
        self.ObjVal = model.ObjVal
        # X_ijk
        self.X = [[([0] * data.vehicleNum) for _ in range(data.nodeNum)] for _ in range(data.nodeNum)]
        # S_ik
        self.S = [([0] * data.vehicleNum) for _ in range(data.nodeNum)]
        # routes
        self.routes = []


def getSolution(data, model):
    solution = Solution(data, model)
    for m in model.getVars():
        split_arr = re.split(r"_", m.VarName)
        if split_arr[0] == 'X' and m.x > 0.5:
            solution.X[int(split_arr[1])][int(split_arr[2])][int(split_arr[3])] = m.x
        elif split_arr[0] == 'S' and m.x > 0.5:
            solution.S[int(split_arr[1])][int(split_arr[2])] = m.x
    for k in range(data.vehicleNum):
        i = 0
        subRoute = []
        subRoute.append(i)
        finish = False
        while not finish:
            for j in range(data.nodeNum):
                if solution.X[i][j][k] > 0.5:
                    subRoute.append(j)
                    i = j
                    if j == data.nodeNum - 1:
                        finish = True
        if len(subRoute) >= 3:
            subRoute[-1] = 0
            solution.routes.append(subRoute)
            solution.routeNum += 1
    return solution


def plot_solution(solution, customer_num):
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title(f"{data_type} : {customer_num} Customers")
    plt.scatter(data.corX[0], data.corY[0], c='blue', alpha=1, marker=',', linewidths=3, label='depot')  # 起点
    plt.scatter(data.corX[1:-1], data.corY[1:-1], c='black', alpha=1, marker='o', linewidths=3,
                label='customer')  # 普通站点

    for k in range(solution.routeNum):
        for i in range(len(solution.routes[k]) - 1):
            a = solution.routes[k][i]
            b = solution.routes[k][i + 1]
            x = [data.corX[a], data.corX[b]]
            y = [data.corY[a], data.corY[b]]
            plt.plot(x, y, 'k', linewidth=1)
    plt.grid(False)
    plt.legend(loc='best')
    plt.show()


def print_solution(solution, data):
    for index, subRoute in enumerate(solution.routes):
        distance = 0
        load = 0
        for i in range(len(subRoute) - 1):
            distance += data.distanceMatrix[subRoute[i]][subRoute[i + 1]]
            load += data.demand[subRoute[i]]
        print(f"Route-{index + 1} : {subRoute} , distance: {distance} , load: {load}")


def solve(data):
    # 声明模型
    model = Model("VRPTW")
    # 模型设置
    # 关闭输出
    model.setParam('OutputFlag', 0)
    # 定义变量
    X = [[[[] for _ in range(data.vehicleNum)] for _ in range(data.nodeNum)] for _ in range(data.nodeNum)]
    S = [[[] for _ in range(data.vehicleNum)] for _ in range(data.nodeNum)]
    for i in range(data.nodeNum):
        for k in range(data.vehicleNum):
            S[i][k] = model.addVar(data.readyTime[i], data.dueTime[i], vtype=GRB.CONTINUOUS, name=f'S_{i}_{k}')
            for j in range(data.nodeNum):
                X[i][j][k] = model.addVar(vtype=GRB.BINARY, name=f"X_{i}_{j}_{k}")
    # 目标函数
    obj = LinExpr(0)
    for i in range(data.nodeNum):
        for j in range(data.nodeNum):
            if i != j:
                for k in range(data.vehicleNum):
                    obj.addTerms(data.distanceMatrix[i][j], X[i][j][k])
    model.setObjective(obj, GRB.MINIMIZE)
    # 约束1：车辆只能从一个点到另一个点
    for i in range(1, data.nodeNum - 1):
        expr = LinExpr(0)
        for j in range(data.nodeNum):
            if i != j:
                for k in range(data.vehicleNum):
                    if i != 0 and i != data.nodeNum - 1:
                        expr.addTerms(1, X[i][j][k])
        model.addConstr(expr == 1)
    # 约束2：车辆必须从仓库出发
    for k in range(data.vehicleNum):
        expr = LinExpr(0)
        for j in range(1, data.nodeNum):
            expr.addTerms(1, X[0][j][k])
        model.addConstr(expr == 1)
    # 约束3：车辆经过一个点就必须离开一个点
    for k in range(data.vehicleNum):
        for h in range(1, data.nodeNum - 1):
            expr1 = LinExpr(0)
            expr2 = LinExpr(0)
            for i in range(data.nodeNum):
                if h != i:
                    expr1.addTerms(1, X[i][h][k])
            for j in range(data.nodeNum):
                if h != j:
                    expr2.addTerms(1, X[h][j][k])
            model.addConstr(expr1 == expr2)
    # 约束4：车辆最终返回仓库
    for k in range(data.vehicleNum):
        expr = LinExpr(0)
        for i in range(data.nodeNum - 1):
            expr.addTerms(1, X[i][data.nodeNum - 1][k])
        model.addConstr(expr == 1)
    # 约束5：车辆容量约束
    for k in range(data.vehicleNum):
        expr = LinExpr(0)
        for i in range(1, data.nodeNum - 1):
            for j in range(data.nodeNum):
                if i != 0 and i != data.nodeNum - 1 and i != j:
                    expr.addTerms(data.demand[i], X[i][j][k])
        model.addConstr(expr <= data.capacity)
    # 约束6：时间窗约束
    for k in range(data.vehicleNum):
        for i in range(data.nodeNum):
            for j in range(data.nodeNum):
                if i != j:
                    model.addConstr(S[i][k] + data.distanceMatrix[i][j] - S[j][k] <= M - M * X[i][j][k])
    # 记录求解开始时间
    start_time = time.time()
    # 求解
    model.optimize()
    if model.status == GRB.OPTIMAL:
        print("-" * 20, "Solved Successfully", '-' * 20)
        # 输出求解总用时
        print(f"Solve Time: {time.time() - start_time} s")
        print(f"Total Travel Distance: {model.ObjVal}")
        solution = getSolution(data, model)
        plot_solution(solution, data.customerNum)
        print_solution(solution, data)
    else:
        print("此题无解")


if __name__ == '__main__':
    # 哪个数据集
    data_type = "c101"
    # 数据集路径
    data_path = f'../../data/solomn_data/{data_type}.txt'
    # 顾客个数设置（从上往下读取完 customerNum 个顾客为止，例如c101文件中有100个顾客点，
    # 但是跑100个顾客点太耗时了，设置这个数是为了只选取一部分顾客点进行计算，用来快速测试算法）
    # 如果想用完整的顾客点进行计算，设置为None即可
    customerNum = 50
    # 一个很大的正数
    M = 10000000
    # 读取数据
    data = readData(data_path, customerNum)
    # 输出相关数据
    print("-" * 20, "Problem Information", '-' * 20)
    print(f'Data Type: {data_type}')
    print(f'Node Num: {data.nodeNum}')
    print(f'Customer Num: {data.customerNum}')
    print(f'Vehicle Num: {data.vehicleNum}')
    print(f'Vehicle Capacity: {data.capacity}')
    # 建模求解
    solve(data)

3.3 Display of running results

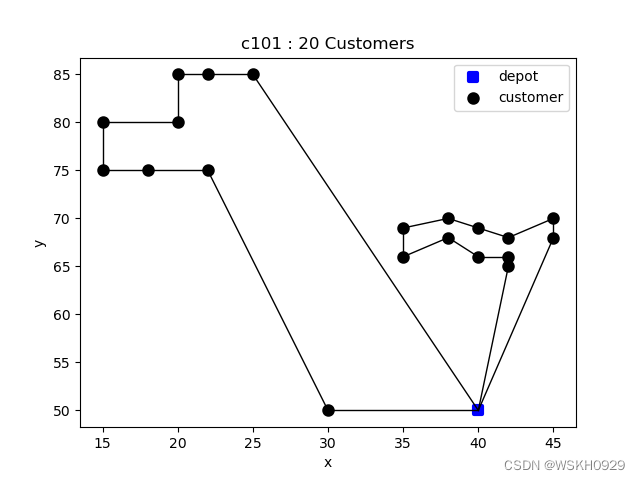
3.3.1 Test case: c101.txt

set customerNum = 20

-------------------- Problem Information --------------------
Data Type: c101
Node Num: 22
Customer Num: 20
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Successfully --------------------
Solve Time: 0.2966279983520508 s
Total Travel Distance: 160.81590595966603
Route-1 : [0, 20, 13, 17, 18, 19, 15, 16, 14, 12, 0] , distance: 101.32767502613292 , load: 200.0
Route-2 : [0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 0] , distance: 59.48823093353308 , load: 160.0

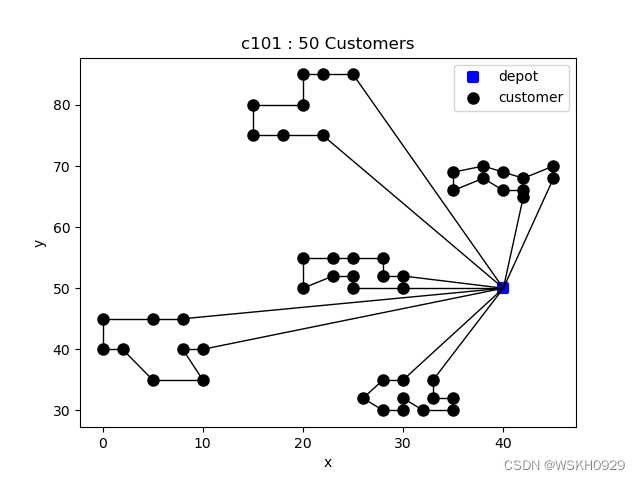
insert image description here

set customerNum = 50

Data Type: c101
Node Num: 52
Customer Num: 50
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Successfully --------------------
Solve Time: 4.383494138717651 s
Total Travel Distance: 363.2468004115909
Route-1 : [0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 0] , distance: 59.48823093353308 , load: 160.0
Route-2 : [0, 32, 33, 31, 35, 37, 38, 39, 36, 34, 0] , distance: 97.2271627850669 , load: 200.0
Route-3 : [0, 43, 42, 41, 40, 44, 46, 45, 48, 50, 49, 47, 0] , distance: 59.843107259523165 , load: 140.0
Route-4 : [0, 20, 24, 25, 27, 29, 30, 28, 26, 23, 22, 21, 0] , distance: 50.80359030264955 , load: 170.0
Route-5 : [0, 13, 17, 18, 19, 15, 16, 14, 12, 0] , distance: 95.88470913081827 , load: 190.0

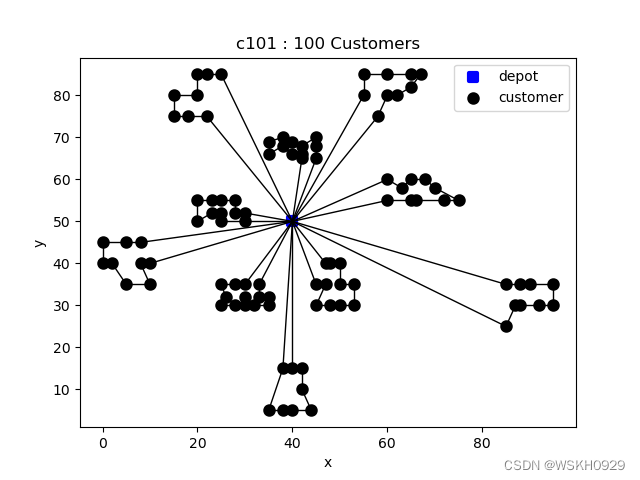
insert image description here

set customerNum = None

-------------------- Problem Information --------------------
Data Type: c101
Node Num: 102
Customer Num: 100
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Successfully --------------------
Solve Time: 272.5895857810974 s
Total Travel Distance: 828.9368669428341
Route-1 : [0, 20, 24, 25, 27, 29, 30, 28, 26, 23, 22, 21, 0] , distance: 50.80359030264955 , load: 170.0
Route-2 : [0, 57, 55, 54, 53, 56, 58, 60, 59, 0] , distance: 101.88256760196126 , load: 200.0
Route-3 : [0, 5, 3, 7, 8, 10, 11, 9, 6, 4, 2, 1, 75, 0] , distance: 59.618077542105574 , load: 180.0
Route-4 : [0, 98, 96, 95, 94, 92, 93, 97, 100, 99, 0] , distance: 95.94313062205805 , load: 190.0
Route-5 : [0, 81, 78, 76, 71, 70, 73, 77, 79, 80, 0] , distance: 127.29748041459519 , load: 150.0
Route-6 : [0, 32, 33, 31, 35, 37, 38, 39, 36, 34, 0] , distance: 97.2271627850669 , load: 200.0
Route-7 : [0, 43, 42, 41, 40, 44, 46, 45, 48, 51, 50, 52, 49, 47, 0] , distance: 64.80747449698114 , load: 160.0
Route-8 : [0, 90, 87, 86, 83, 82, 84, 85, 88, 89, 91, 0] , distance: 76.06956532288787 , load: 170.0
Route-9 : [0, 13, 17, 18, 19, 15, 16, 14, 12, 0] , distance: 95.88470913081827 , load: 190.0
Route-10 : [0, 67, 65, 63, 62, 74, 72, 61, 64, 68, 66, 69, 0] , distance: 59.403108723710105 , load: 200.0

insert image description here

3.3.2 Test case: r101.txt

set customerNum = 20

-------------------- Problem Information --------------------
Data Type: r101
Node Num: 22
Customer Num: 20
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Successfully --------------------
Solve Time: 0.9535932540893555 s
Total Travel Distance: 463.69270291007086
Route-1 : [0, 9, 20, 1, 0] , distance: 74.91992978886165 , load: 35.0
Route-2 : [0, 12, 3, 4, 0] , distance: 76.18033988749895 , load: 51.0
Route-3 : [0, 2, 15, 13, 0] , distance: 62.180339887498945 , load: 38.0
Route-4 : [0, 5, 18, 8, 17, 0] , distance: 86.57837545317302 , load: 49.0
Route-5 : [0, 14, 16, 6, 0] , distance: 72.40405733948208 , load: 42.0
Route-6 : [0, 11, 19, 7, 10, 0] , distance: 91.42966055355615 , load: 50.0

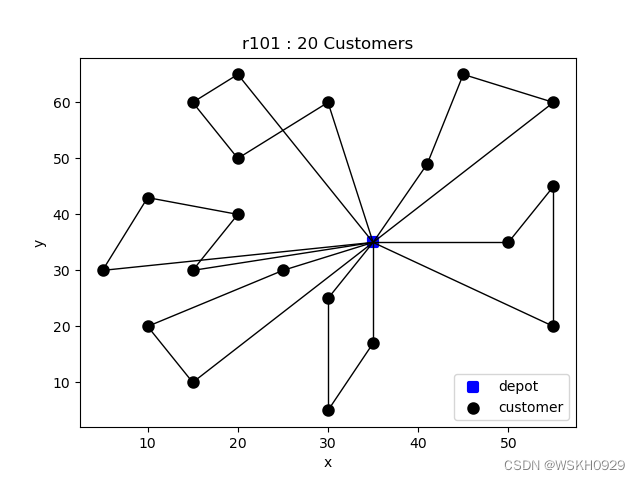
insert image description here

set customerNum = 50

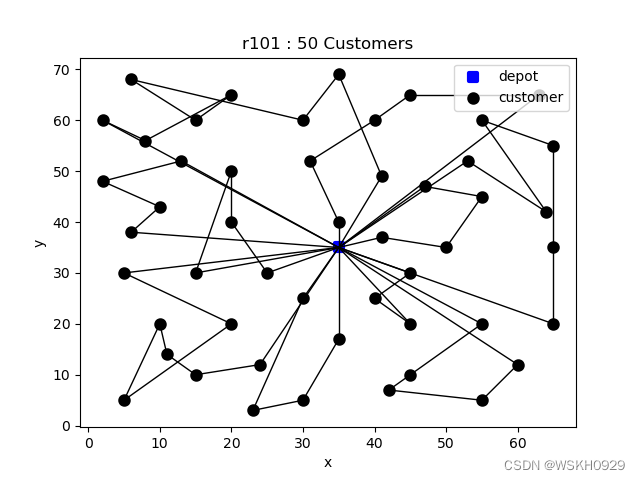
-------------------- Problem Information --------------------
Data Type: r101
Node Num: 52
Customer Num: 50
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Successfully --------------------
Solve Time: 4.6791017055511475 s
Total Travel Distance: 946.6603871872358
Route-1 : [0, 21, 40, 26, 0] , distance: 43.35023188854984 , load: 37.0
Route-2 : [0, 33, 29, 9, 34, 24, 25, 0] , distance: 139.4708769010923 , load: 59.0
Route-3 : [0, 39, 23, 41, 22, 4, 0] , distance: 99.11062351878482 , load: 102.0
Route-4 : [0, 28, 12, 3, 50, 0] , distance: 51.94121366484106 , load: 61.0
Route-5 : [0, 36, 47, 11, 19, 49, 10, 32, 1, 0] , distance: 154.4302586824376 , load: 140.0
Route-6 : [0, 42, 14, 44, 16, 38, 37, 17, 0] , distance: 131.9204195702968 , load: 88.0
Route-7 : [0, 2, 15, 43, 13, 0] , distance: 72.54724253800985 , load: 45.0
Route-8 : [0, 45, 8, 46, 48, 0] , distance: 84.49944230335126 , load: 62.0
Route-9 : [0, 5, 7, 18, 6, 0] , distance: 73.5917360311745 , load: 46.0
Route-10 : [0, 27, 31, 30, 20, 35, 0] , distance: 95.79834208869767 , load: 81.0

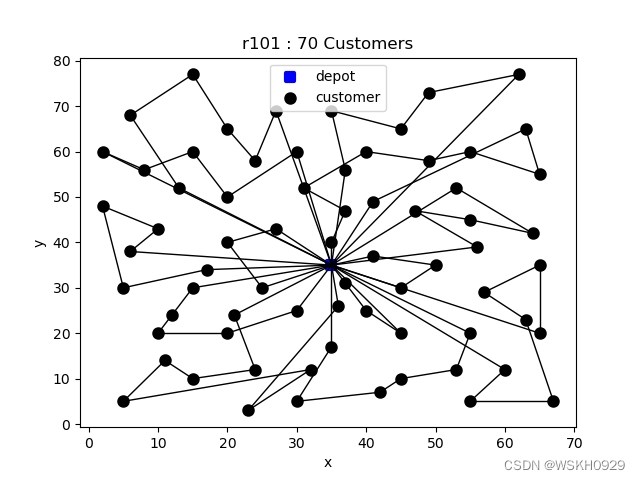
insert image description here

set customerNum = 70

-------------------- Problem Information --------------------
Data Type: r101
Node Num: 72
Customer Num: 70
Vehicle Num: 25
Vehicle Capacity: 200.0
-------------------- Solved Successfully --------------------
Solve Time: 189.01783299446106 s
Total Travel Distance: 1182.9787814963945
Route-1 : [0, 63, 62, 11, 64, 49, 48, 0] , distance: 125.38755919928242 , load: 116.0
Route-2 : [0, 65, 66, 20, 32, 70, 0] , distance: 117.49399251197822 , load: 82.0
Route-3 : [0, 28, 12, 26, 0] , distance: 33.795507476994075 , load: 52.0
Route-4 : [0, 33, 29, 3, 50, 68, 0] , distance: 90.77710269056311 , load: 82.0
Route-5 : [0, 2, 15, 41, 22, 56, 4, 0] , distance: 88.90058825018636 , load: 63.0
Route-6 : [0, 27, 69, 31, 30, 51, 9, 34, 35, 1, 0] , distance: 111.48892006549234 , load: 128.0
Route-7 : [0, 45, 8, 46, 17, 60, 0] , distance: 93.91701945260407 , load: 31.0
Route-8 : [0, 59, 42, 14, 44, 38, 57, 43, 58, 0] , distance: 131.96251141349887 , load: 119.0
Route-9 : [0, 39, 23, 67, 55, 54, 24, 25, 0] , distance: 140.03829072128988 , load: 114.0
Route-10 : [0, 52, 18, 6, 0] , distance: 41.290161379846566 , load: 24.0
Route-11 : [0, 36, 47, 19, 7, 10, 0] , distance: 107.49141646738926 , load: 70.0
Route-12 : [0, 21, 40, 53, 0] , distance: 36.27916407668437 , load: 34.0
Route-13 : [0, 5, 61, 16, 37, 13, 0] , distance: 64.15654779058515 , load: 89.0